2. Волновые свойства вещества
Задача №3.
Параллельный пучок электронов, разогнанных в электрическом поле с разностью потенциалов 15В, падает на узкую прямоугольную диафрагму шириной 0,008 нм. Найти ширину главного дифракционного максимума на экране, расположенном на расстоянии 60 м от диафрагмы.
|
Дано: φ=15 В a=0,08 мм l=60 cм |
Решение: 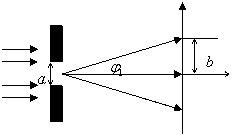 |
|---|---|
|
Найти: b=? |
Чтобы найти ширину главного дифракционного максимума, воспользуемся формулой
asinφ1=λ, |
(1) |
где λ - длина волны, φ1 - первый дифракционный угол, a - ширина диафрагмы. Длина волны определяется соотношением де Бройля
\( \lambda=\frac{h}{p} \), |
(2) |
где p - импульс частицы. Кинетическая энергия электрона, которую он получил при разгоне в поле, равна
T=eφ=15 эВ. |
(3) |
Следовательно, движение электрона нерелятивистское, и импульс частицы определяется формулой
\( p=\sqrt{2mT} \). |
(4) |
Дифракционный угол φ1 определим из геометрии движения электрона после прохождения диафрагмы
\( tg{ \varphi}_1=\frac{b}{2l} \). |
(5) |
Поскольку дифракционный угол φ1 мал, то (5) можно заменить другим соотношением
\( sin{\varphi}_1\approx\frac{b}{2l} \). |
(6) |
Применяя формулу (1), (2). (4) и (6), получим выражение для ширины дифракционного максимума b на экране:
\( b=2lsin{\varphi}_1=2l\frac{\lambda}{a}=\frac{2lh}{a\sqrt{2mT}} \). |
(7) |
Расчет:
\( b=\frac{2\cdot0,6\cdot6,626\cdot10^{-34}}{8\cdot10^{-5}\cdot\sqrt{2\cdot0,911\cdot10^{-30}\cdot15\cdot1,602\cdot10^{-19}}}=4,749\cdot10^{-6} \)м=4,8мкм. |