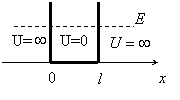3. Уравнение Шредингера. Волновая функция
Примеры решения задач
| Сайт: | Система электронного и дистанционного обучения СВФУ |
| Курс: | Физика атома и ядра. Слепцов И.А., Слепцов А.А. |
| Книга: | 3. Уравнение Шредингера. Волновая функция |
| Напечатано:: | Гость |
| Дата: | Tuesday, 23 July 2024, 08:26 |
Примеры решения задач
Задача №1.
Задана пси - функция ψ(x,y,z) частицы. Написать выражение вероятности того, что частица будет обнаружена в области объема V.
Задача №2.
Найти пси - функции и значения энергии частицы массы m, находящейся в одномерной бесконечно глубокой потенциальной яме ширины l.
Задача №3.
Волновая функция частица массы U(x)=kx2/2 для основного состояния в одномерном потенциальном поле имеет вид ψ(x)=Aexp(-αx2), где A и - некоторые постоянные. Найти с помощью уравнения Шрёдингера постоянную α и энергию E частицы в этом состоянии.
Задача №4.
Электроны, обладающие энергией E=16,0 эВ, на своем пути встречают прямоугольный потенциальный барьер высотой U0=4,0 эВ. Найти коэффициент отражения R и коэффициент D пропускания волн де Бройля для данного барьера.
Задача №5.
Найти вероятность просачивания электрона через потенциальный барьер шириной 5 Å и высотой 0,4 эВ, если он разгоняется электрическим полем 0,3В.
Задача №1.
Задана пси - функция ψ(x,y,z) частицы. Написать выражение вероятности того, что частица будет обнаружена в области объема V.
|
Дано: ψ(x,y,z) |
Решение: |
|---|---|
|
Найти: P=? |
Координатной волновой функции ψ(x,y,z), которая является решением стационарного уравнения Шрёдингера, задается статистическое толкование: квадрат модуля волновой функции есть плотность вероятности найти частицу в элементарном объеме около точки (x,y,z). Сама вероятность определяется соотношением
dP=|ψ(x,y,z)|2dxdydz=ψ*(x,y,z)ψ(x,y,z)dxdydz. |
(1) |
Если частица находится около данной точки объема, его нахождение в других местах исключено. Следовательно, нахождения частицы в данный момент времени в разных местах объема являются исключающими друг друга событиями. И вероятность того, что осуществится какое - либо из этих событий, равна сумме вероятностей всех этих событий. Следовательно, вероятность найти частицу около одной из точек области пространства, ограниченной объемом V, равна интегралу по всему заданному объему
\( \int{dP}={\int}_V \psi^*\psi{d}\tau \), |
(2) |
где dτ=dxdydz.
Задача №2.
Найти пси - функции и значения энергии частицы массы m, находящейся в одномерной бесконечно глубокой потенциальной яме ширины l.
|
Дано: m, l |
Решение: |
|---|---|
|
Найти: ψn=? En=? |
Потенциальная яма есть график одномерной ступенчатой функции потенциальной энергии частицы
|
(1) |
График функции (1) имеет вид
|
Вне ямы (x≤0, x≥l) функция ψ(x) равна нулю. Движение частицы в яме описывается одномерным уравнением Шрёдингера
\( \frac{d\psi(x)}{dx^2}+\frac{2m}{{\hbar}^2}E\psi(x)=0 \). |
(2) |
Дополнительными условиями в задаче будут следующие граничные условия:
ψ(0)=ψ(l)=0. |
(3) |
Вводим новый параметр уравнения
\( {\omega}^2=\frac{2mE}{{\hbar}^2} \). |
(4) |
Тогда уравнение примет вид
\( \frac{d \psi(x)}{dx^2}+{\omega}^2\psi{x}=0 \). |
(5) |
Известно, что такое уравнение имеет действительные решения
ψ(x)=Asinωx+Bcosωx. |
(6) |
Необходимо определить коэффициенты A,B и параметр ω. Чтобы соблюсти условие ψ(0)=0, полагаем что, B=0. Из второго граничного условие следует, что
\( \omega= \pm\frac{n\pi}{l}, n=0,1,... \) |
(7) |
Используя полученное выражение (7), из определения (4) параметра ω находим выражение для возможных энергетических уровней частицы, движущейся в бесконечно глубокой потенциальной яме
\( E_n=\frac{{\pi}^2{\hbar}^2}{2ml^2}n^2 \), n=1,2,... |
(8) |
Найденным собственным значениям энергии En соответствуют собственные волновые функции ψn(x) вида
\( { \psi }_n(x)=Asin\frac{n\pi}{l}x \). |
(9) |
Из условия нормировки волновой функции к единице
\( A^2{\int}_{0}^{l}{sin}^2\frac{n\pi}{l}xdx=1 \) |
(10) |
находим коэффициент A. Вычислив интеграл (10), получим
\( A=\sqrt{\frac{2}{l}} \). |
(11) |
Итак, выражение для собственных функций ψn(x) энергии частицы в бесконечно глубокой потенциальной яме имеет вид
\( {\psi}_n(x)=\sqrt{\frac{2}{l}}sin\frac{n\pi}{l}x \), n=1,2,... |
(12) |
Задача №3.
Волновая функция частица массы U(x)=kx2/2 для основного состояния в одномерном потенциальном поле имеет вид ψ(x)=Aexp(-αx2), где A и - некоторые постоянные. Найти с помощью уравнения Шрёдингера постоянную α и энергию E частицы в этом состоянии.
|
Дано: \( U(x)=\frac{kx^2}{2} \) ψ(x)=Ae-αx2 |
Решение: |
|---|---|
|
Найти: α=? En=? |
В данном случае одномерное стационарное уравнение Шрёдингера имеет вид
\( \frac{d^2\psi(x)}{dx^2}+\frac{2m}{{\hbar}^2}\left(E-\frac{kx^2}{2}\right)\psi(x)=0 \). |
(1) |
Частота квазиупругих колебаний определяется соотношением
\( \omega=\sqrt{\frac{k}{m}} \), |
(2) |
где k - коэффициент квазиупругости. Отсюда следует
\( \frac{d\psi(x)}{dx^2}+\frac{2m}{{\hbar}^2}E\psi(x)=0 \). |
(3) |
где
\( \lambda=\frac{2mE}{{\hbar}^2} \), \( { \xi}^2=\frac{m^2{\omega}^2}{{\hbar}^2} \). |
(4) |
От заданной функции
ψ(x)=Ae-αx2 |
(5) |
берем первую и вторую производные. Они равны
\( \frac{d\psi}{dx}=-2\alpha{A}e^{-{\alpha}x^2} \), |
(6) |
\( \frac{d^2\psi}{dx^2}=-2\alpha{A}e^{-{\alpha}x^2}+4{\alpha}^2x^2\alpha{A}e^{-{\alpha}x^2} \). |
(7) |
Поставив (5) и (7) в уравнение (3) получим тождество
(4α2-ξ2)x2+(λ-2α)=0. |
(8) |
Чтобы определить параметры α и ξ из тождества (8), воспользуемся способом неопределенных коэффициентов. Суть метода состоит в том, что многочлены при различных степенях x приравняют нулю и получают систему алгебраических уравнений
4α2-ξ2=0, |
(9) |
λ-2α=0. |
(10) |
Из системы получаем равенство
α2=ξ2. |
(11) |
Поставляя значения параметров из формул (4) в равенство (11), находим
\( E=\sqrt{\frac{{\omega}^2{\hbar}^2}{4}}=\frac{{\omega}{\hbar}}{2} \), (E>0). |
(12) |
Из уравнения (10) находим
\( \alpha=\frac{\lambda}{2}=\frac{m\omega}{2\hbar} \). |
(13) |
Задача №4.
Электроны, обладающие энергией E=16,0 эВ, на своем пути встречают прямоугольный потенциальный барьер высотой U0=4,0 эВ. Найти коэффициент отражения R и коэффициент D пропускания волн де Бройля для данного барьера.
|
Дано: E=16,0 эВ U0=4,0 эВ |
Решение: 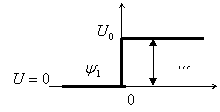 |
|---|---|
|
Найти: R=? D=? |
В задаче рассматривается случай перехода частицы в безгранично протяженную область с потенциальной энергией U0. Притом имеет место условие E>U0. Напишем уравнение Шрёдингера отдельно для каждой из смежных областей, на которые разделено пространство барьером. Свободное движение частицы до барьера описывается равнением
\( \frac{d^2{\psi}_1}{dx^2}+\frac{2mE}{{\hbar}^2}{\psi}_1=0 \). |
(1) |
Уравнение движения частицы внутри барьера высотой U0 имеет вид
\( \frac{d^2{\psi}_2}{dx^2}+\frac{2m(E-U_0)}{{\hbar}^2}{\psi}_2=0 \). |
(2) |
Вводя новые параметры
\( k_1=\frac{2mE}{{\hbar}^2} \) и \( k_2=\frac{2m(E-U_0)}{{\hbar}^2} \), |
(3) |
перепишем уравнения (1) и (2) следующим образом:
\( \frac{d^2{\psi}_1}{dx^2}+k^2_1{\psi}_1=0 \), |
(4) |
\( \frac{d^2{\psi}_2}{dx^2}+k^2_2{\psi}_2=0 \). |
(5) |
Решения уравнения (4) и (5) ищутся общепринятым в математике методом. Решения уравнений пишут в комплексной форме. Оно для уравнения (4) имеет следующий вид:
ψ1=A1eik1x+B1e-ik1x. |
(6) |
Отсюда следует, что волновая функция ψ1(x) представляет собой наложение двух противоположно направленных волн. После столкновения со стенкой барьера частица либо не изменит прежнего направления движения (x>0), либо изменит его в другую сторону (x<0). Решение уравнения (5) имеет вид
ψ2=A2eik1x. |
(7) |
Функция ψ2 не содержит второго члена, поскольку в барьере бесконечной ширины частица не сталкивается ни с чем, и продолжает свое движение по первоначальному движению. Классическое определение коэффициента R отражения определяется отношением плотностей n′ и n потоков частиц, отраженных от барьера и упавших на него, которые в свою очередь пропорциональны соответствующим вероятностям:
\( R=\frac{n'}{n}=\frac{|B_1|^2}{|A_1|^2} \). |
(8) |
Отсюда ясно, что коэффициент R следует трактовать как вероятность отражения частицы от стенки барьера. Далее воспользуемся условиями «сшивания» для функций ψ1 и ψ2
ψ1(0)=ψ2(0), |
(9) |
\( \frac{{\psi}_1}{dx}|_{x=0}=\frac{{\psi}_2}{dx}|_{x=0} \) |
(10) |
Эти условия непрерывности функции и также и ее первой производной дают возможность довести решение задачи до конца. Подстановка решений (6) и (7) в условиях «сшивания» функций дает систему из двух уравнений с тремя неизвестными
A1+B1=A2, |
(11) |
k1A1-k1B1=k2A2. |
(12) |
Чтобы найти соотношение коэффициентов B1/A1 исключим из системы A2. Для этого делим (12) на коэффициент k2, вычтем его из (11), и получим следующее равенство:
\( \left(1+\frac{k_1}{k_2}\right)B_1=\left(\frac{k_1}{k_2}-1\right)A_1 \). |
(13) |
Отсюда имеем
\( R={\left|\frac{B_1}{A_1}\right|}^2=\frac{{(k_1-k_2)}^2}{{(k_1+k_2)}^2} \). |
(14) |
Заметим, что частица, ударившись об стенку барьера, либо отразится, либо пройдет дальше в барьер. Следовательно, коэффициент пропускания D, то есть вероятность того, что частица попадет в барьер бесконечной ширины, можно определить из суммы вероятностей двух взаимно исключающих друг друга событий
\( D+1-R=\frac{4k_1k_2}{{(k_1+k_2)}^2} \). |
(15) |
Поставив в (15) значения коэффициентов k1 и k2, найдем выражение для расчета D. Оно имеет вид
\( D=\frac{4\sqrt{E(E-U_0)}}{{(\sqrt{E}-\sqrt{E-U_o})}^2} \). |
(16) |
Расчет:
\( D=\frac{4\sqrt{16\cdot12}}{{(4+\sqrt{12})}^2}=\frac{55,4256}{55,7128}=0,9948\approx99,5 \)%, R=1-0,9948=0,0051≈0,5%. |
Задача №5.
Найти вероятность просачивания электрона через потенциальный барьер шириной 5 Å и высотой 0,4 эВ, если он разгоняется электрическим полем 0,3В.
|
Дано: U0=0,4 эВ, φ=0,3 эВ, l=5 Å |
Решение: 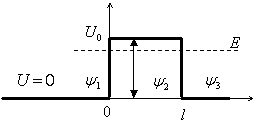 |
|---|---|
|
Найти: P=? |
Потенциальный барьер конечной ширины разделяет пространство на три смежные области, в которых состояние частицы описывается тремя различными функциями. В соответствии с этим имеем три уравнения Шрёдингера:
\( \frac{d^2{\psi}_1}{dx^2}+k_1{\psi}_1=0 \) для первой области, |
(1) |
\( \frac{d^2{\psi}_2}{dx^2}-k_2{\psi}_2=0 \) для второй области, |
(2) |
\( \frac{d^2{\psi}_3}{dx^2}+k_3{\psi}_3=0 \) для третьей области. |
(3) |
Для первой и третьей областей ввели обозначения коэффициентов
\( k_1^2=k_3^2=\frac{2mE}{{\hbar}^2} \). |
(4) |
При учете условия E<U0 аналогичный коэффициент для второй области имеет вид
\( k_3^2=\frac{2m(U_0-E)}{{\hbar}^2} \). |
(5) |
Общие решения уравнения в трех смежных областях:
ψ1=A1eik1x+B1e-ik1x для первой области, |
(6) |
ψ2=A2ek2x+B2e-k2x для второй области, |
(7) |
ψ3=A3eik3x+B3e-ik3x для третьей области. |
(8) |
В двух первых областях часть падающих частиц отражаются обратно, а в третьей такого отражения нет. Следовательно, коэффициент B3 нужно приравнять нулю. Чтобы найти соотношения, связывающие амплитудные коэффициенты A1,B1,A2,B2,A3, необходимо использовать условия «сшивания» функций на границах областей:
ψ1(0)=ψ2(0), ψ2(l)=ψ3(l) |
(9) |
\( \frac{d\psi_1}{dx}|_{x=0}=\frac{d\psi_2}{dx}|_{x=0} \), \( \frac{d\psi_2}{dx}|_{x=l}=\frac{d\psi_3}{dx}|_{x=l} \). |
(10) |
Тогда получим систему алгебраических уравнений
A1+B1=A2+B2, |
(11) |
A2ek2l+B2e-k2l=A3eik3l, |
(12) |
ik1A1-ik1B1=k2A2-k2B2, |
(13) |
k2A2ek2l-k2B2e-k2l=ik3A3ek3l. |
(14) |
Вероятность просачивания частицы через потенциальный барьер определяется коэффициентом D прозрачности барьера
\( D=\frac{{|A_3|}^2}{|A_1|}=\frac{A_3^*A_3}{|A_1|} \). |
(15) |
Следовательно, нас интересуют коэффициенты A3 и A1. Поскольку падение частицы на барьер является достоверным событием, можно полагать амплитуду A1 волны, падающей на барьер, равным единице. А коэффициент A3 можно найти, решая систему уравнений (11) - (14). Для этого необходимо из системы (11) - (14) составить систему из трех уравнений, первое из которых имеет вид
1+B1=A2+B2. |
(11a) |
Умножим уравнение (11а) на мнимую единицу i и сложим с уравнением (13). Это дает второе искомое уравнение
(n+i)A2-(n-i)B2=2i, |
(16) |
где n=k2/k1. Теперь умножим уравнение (12) на число i и вычтем его из уравнения (14). В результате получим
(n-i)ek2lA2-(n+i)e-k2lB2. |
(17) |
Корни системы (11а -17) имеют вид
\( A_2=\frac{2i(n+i)e^{-k_2l}}{{(n+i)}^2e^{-k_2l}-{(n-i)}^2e^{k_2l}} \), |
(18) |
\( B_2=\frac{2i(n-i)e^{k_2l}}{{(n+i)}^2e^{-k_2l}-{(n-i)}^2e^{k_2l}} \), |
(19) |
\( A_3=\frac{4ine^{-ik_1l}}{{(n+i)}^2e^{-k_2l}-{(n-i)}^2e^{k_2l}} \). |
(20) |
Обычно условие k2l>>1 выполняется, поэтому первым слагаемым в знаменателе дроби (20) можно пренебречь. Тогда имеем
\( A_3\approx-\frac{4ine^{-ik_1l}}{{(n-i)}^2}e^{-k_2l} \). |
(21) |
Поставляя (21) в (15), находим
\( D\approx-\frac{4ine^{-ik_1l}}{{(n-i)}^2}e^{-k_2l}{\cdot}\frac{4ine^{ik_1l}}{{(n+i)}^2}e^{-k_2l}=\frac{16n^{2}}{{(n^2+1)}^2}e^{-2k_2l} \). |
(22) |
Здесь учтено, что \( {|n-i|}^2=(n-i)(n+i)=\sqrt{n^2+1} \).
Следовательно, имеем
\( D\approx\frac{16n^{2}}{{(n^2+1)}^2}e^{-\frac{2}{\hbar}\sqrt{2m(U_0-E)}l} \). |
(23) |
Вычислим величину n2, выразив ее через величины U0 и E:
\( n^2=\frac{k_2^2}{k_1^2}=\frac{U_0-E}{E}=\frac{U_0}{E}-1=\frac{0,4}{0,3}-1=0,333 \). |
Расчет:
\( D=\frac{16\cdot{0,333}^2}{{(0,333+1)}^2}\cdot{exp}\left(\frac{2\cdot5\cdot10^{-10}}{1,0546\cdot10^{-34}}\cdot\sqrt{2\cdot0,911\cdot10^{-30}\cdot(0,4-0,3)\cdot1,6\cdot10^{-19}}\right)=0,9985\cdot{exp}(-1,618999)=0,9985\cdot0,198097=0,19779\approx0,2=20 \)% |
По поводу полученного результата сделаем следующее замечание. Расчет показал, что коэффициент перед экспонентой имеет величину порядка единицы. В данном случае это не является исключением. Поэтому в формуле (23) не пишут его как несущественный множитель, и коэффициент просачивания частицы через прямоугольный барьер конечной ширины представляют в виде
\( D\approx{e}^{\frac{2}{\hbar}\sqrt{2m(U_o-E)}l} \). |
(24) |