Физика атома и ядра. Слепцов И.А., Слепцов А.А.

Микрочастицы.

Микрочастицами называют элементарные частицы, а также сложные частицы, образованные из сравнительно небольшого числа элементарных частиц. К элементарным частицам относят электроны, протоны, нейтроны, фотоны и другие частицы, обнаруженные при ядерных исследованиях. К сложным микрочастицам относят молекулы, атомы, атомные ядра и ряд других образований.

Микрочастица является чисто квантовой частицей, то есть движение такой частицы подчиняется квантовым законам. Она представляет собой образование особого рода, которая обладает в единой связи корпускулярно-волновыми свойствами. Отличие микрочастицы от классической частицы заключается в том, что она не обладает одновременно определенными значениями координат и импульса, то есть понятие траектории теряет своего физического смысла. В то же время микрочастицы всегда обнаруживается как целое, с присущей ему массой, зарядом и другими характерными для него величинами.

Гипотезы де Бройля.

Де Бройль предположил, что материальные частицы должны обладать такими же двойственными свойствами, как частицы световой волны - фотоны. Он приписал микрочастице энергию, равную

Здесь ν или ω являются частотами того волнового процесса, который сопоставляется движению частицы. Смысл гипотезы заключается в том, что микрочастица обладает свойствами, которые одновременно характеризуются и механическими, и волновыми величинами. Исходя из релятивистского выражения для энергии частицы, де Бройль предложил еще одно соотношение

где p, λ - импульс частицы и длина волны соответствующего волнового процесса, h - постоянная величина, введенная Планком в теории теплового излучения. Волна де Бройля отвечает тем же законам для фазовых и групповых скоростей волны, что имеется в классической волновой теории. Для нее можно получить соответствующие законы дисперсии в релятивистской и нерелятивистской форме. Закон дисперсии устанавливает связь между частотой ω волны и составляющими волнового вектора k_x,k_y,k_z. Для этого достаточно переписать релятивистский закон связи между энергией частицы и ее импульсов в терминах гипотезы де Бройля. Квадрат полной энергии релятивисткой частицы равен

Используя соотношения (1) и (2), нетрудно получить закон дисперсии

Для фотона - частицы световой волны этот закон запишется следующим образом:

Здесь учтено что, для фотона E₀=0. С другой стороны, формула (4а) следует из волнового уравнения, решением которого служит формула плоской волны

Де Бройль предложил описать движение свободной материальной частицы этой же формулой, поэтому она носит название волны де Бройля. Де Бройль также переписал условие квантования орбиты в новом виде

где r - радиус орбиты электрона в атоме Бора.

Принцип неопределенности.

Рассмотрим следующую ситуацию. Поток микрочастиц летит по некоторому определенному направлению, например, по оси Oy. На пути потока поставим непроницаемую тяжелую диафрагму со щелью, ширина которой равна Δx. До момента прохождения щели некоторая микрочастица из потока будет иметь неопределенную координату по оси Ox. Поэтому неопределенность координаты по данной оси будет равна бесконечности Δx=∞. Зато составляющая импульса по этой оси равна нулю, поскольку частицы летит прямо по направлению оси Oy. Следовательно, неопределенность Δp_x=0. В момент прохождения щели микрочастица будет испытать дифракции и отклонится от первоначального направления движения, в результате появится составляющая импульса Δp_x по оси Ox. Неопределенность составляющей импульса будет равна самой этой величине Δp_x=Δp_x.

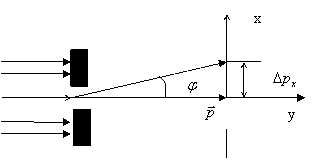
рис. 2

Геометрия рисунка (рис. 2) дает

Здесь учтено, что φ - малая величина. Если угол φ=φ₁ определяет направление первого минимума интенсивности, то имеем

Совместно решая уравнения (7) и (8), получим

Используя соотношения де Бройля между импульсом частицы и соответствующей ее движению длины волны, имеем

При произвольном дифракционном угле φ≥φ₁ равенство (4) нужно записать в виде нестрогого равенства. Поскольку полученное равенство дает оценку лишь по порядку величины, окончательно, искомое соотношение будет иметь вид

Формула (11) называется соотношением неопределенностей двух сопряженных величин p_x и x, соотношением Гайзенберга. Таким образом, произведение неопределенностей двух сопряженных величин по величине порядка не может быть меньше, чем постоянная величина Планка-Дирака. Это утверждение называется принципом Гайзенберга. Формулу можно получить и для двух других координат и соответствующих им составляющих импульса:

Соотношения (11) и (12) выражают принцип неопределенности Гайзенберга: в природе не существуют такие состояния микрообъектов, в которых одновременно можно определить и координату, и соответствующую ей составляющую импульса. Принцип определяет допустимый предел неточностей, с которыми можно характеризовать состояния микрочастицы классически, то есть координатой и соответствующей составляющей импульса. Имеет место еще одно соотношение неопределенностей

Соотношение означает, что нельзя точно определить значение энергии за бесконечно малый промежуток времени. Определение энергии с точностью ΔE должно занять некоторый интервал времени, равный, по меньшей мере, Δt∼ћ/ΔE.

Естественная ширина спектральных линий.

Согласно формуле (13) каждый уровень энергии характеризуется интервалом ΔE_n - шириной уровня. Каждый квантовый переход характеризуется разностью интервалов ΔE_nm двух уровней, между которыми происходит переход. Это разность интервалов называется шириной спектральной линии. Если излучающая система покоится, то ширина линии называется естественной.

Поскольку неопределенность энергии связана с временем жизни состояния соотношением

то ширина спектральных линий равна