4. Спектры. Свойства атомов
Задача №3.
Коротковолновой границе главной серии атома натрия отвечает длина волны λ=243 нм. Найти:
а) потенциал ионизации φi(В) атома;
б) ридберговскую поправку σ(s).
|
Дано: λ=243 нм |
Решение: 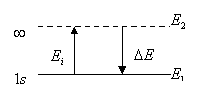 |
|---|---|
|
Найти: φi(B)=? σ(s)=? |
а) Потенциал ионизации равен
\( \varphi_i=\frac{E_i}{e} \), |
(1) |
где e - элементарный заряд, равный абсолютной величине заряда электрона. Коротковолновой линии соответствует переход с основного уровня на уровень «бесконечность». Энергия этого перехода будет ионизационной энергией атома
\( E_i=\Delta{E}=\frac{hc}{\lambda} \). |
(2) |
Здесь мы допустили, что энергия ΔE излучается в виде вылетающего фотона.
б) Энергия ΔE перехода есть разность уровней энергии, соответствующих данному переходу. Следовательно, имеем
Ei=ΔE=E(∞)-E(3s)=-E(3s). |
(3) |
Из сопоставления формул (2) и (3) получаем
\( \frac{hc}{\lambda}=-E(3s) \). |
(4) |
Применяя соотношение Бора между спектральным термом и соответствующим уровнем энергии, эмпирическую формулу Ридберга для терма щелочных металлов, перепишем (3) следующим образом:
\( \frac{hc}{\lambda}=\frac{chR}{{[n+\sigma(s)]}^2} \). |
(5) |
Решая уравнение (5), находим
\( \sigma(s)=\sqrt{\lambda{R}}-n \). |
(6) |
Расчет:
a) \( \varphi_i=\frac{2,998\cdot10^8\cdot6,626\cdot10^{-34}}{243\cdot10^9\cdot1,6\cdot10^{-19}}=5,109=5,1 \), |
|
б) \( \sigma(s)=\sqrt{243\cdot10^{-9}\cdot1,097\cdot10^7}-3=-1,367\approx-1,37 \). |

