4. Спектры. Свойства атомов
Задача №6.
Некоторое количество атомарного водорода находится в тепловом равновесии при температуре T=3000K. Сколько N атомов находится в основном состоянии, приходящихся на один атом в первом возбужденном состоянии.
|
Дано: T=3000 K |
Решение: 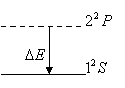 |
|---|---|
|
Найти: N=? |
Наиболее вероятное распределение частиц газа по различным уровням энергии определяется распределением Больцмана
\( \frac{N_2}{N_1}=\frac{\mathrm{g_2}}{\mathrm{g_1}}exp\left(-\frac{E_2-E_1}{kT}\right) \), |
(1) |
где N2, N1, число частиц, обладающих энергиями E2 и E1 соответственно, g1 и g2 - статистические веса (кратности вырождения) уровней 1 и 2. Разность уровней равна энергии перехода
ΔE=E2-E1=ћω. |
(2) |
Отсюда следует, чтоискомая величина равна
\( N=\frac{N_1}{N_2}=\frac{\mathrm{g_1}}{\mathrm{g_2}}exp\left(\frac{\hbar\omega}{kT}\right) \). |
(3) |
Кратность вырождения уровня Ei атома водорода определяется соотношением
gi(l)=2(2l+1). |
(4) |
Частота перехода задается формулой Бальмера - Ридберга
\( \omega=\hbar{R'}\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right) \). |
(5) |
Поставляя (5) и (4) в (3), получим
\( N=\frac{2l_1+1}{2l_2+1}exp\left(\frac{\hbar{R'}}{kT}\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\right) \). |
(6) |
Из диаграммы квантового перехода имеем n1=1, l1=0, n2=2, l2=1. Следовательно, расчетная формула для величины N имеет вид
\( N=\frac{1}{3}exp\left(\frac{3\hbar{R'}}{4kT}\right) \). |
(7) |
Расчеты:
\( N=\frac{1}{3}exp\left(\frac{3\cdot1,0546\cdot10^{-34}\cdot2,07\cdot10^{17}}{4\cdot1,3807\cdot10^{-23}\cdot3000}\right)=\frac{1,4674}{3}=4,89\cdot10^{17} \). |

