4. Спектры. Свойства атомов
Задача №9.
Атом находится в магнитном поле с индукцией B=1Тл. Найти полное расщепление δE (в эВ) термов:
а) 1S, б) 1P, в) 1D, г) 2D5/2.
|
Дано: 1S, 1P, 1D, 1D5/2. |
Решение: 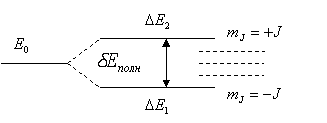 |
|---|---|
|
Найти: δEполн=? |
Атом, обладающий магнитным моментом μJ, в магнитном поле приобретает дополнительную энергию
ΔE=μБgBmJ, mJ=0,±1,...,±J. |
(1) |
Тем самым уровень E0 энергии атома, соответствующий терму кXJ, в магнитном поле расщепляется на равностоящие подуровни. Величина полного расщепления равна
δEполн=ΔE2-ΔE1=2μБgBJ. |
(2) |
Магнетон Бора равен
\( \mu_Б=\frac{0,9274\cdot10^{-23}Дж/Тл}{1,6\cdot10^{-19}Дж/эВ}=5,79625 \)эВ/Тл. |
В термах синглетного типа:
S=0, J=L, g=1, δEполн=2μБBL. |
(3) |
а) Для 1S - терма орбитальное квантовое число L=0, следовательно, δEполн=0.
б) Для 1P - терма L=1, δEполн=2μБB.
б) Для 1D - терма L=2, δEполн=4μБB.
Расчеты:
\( \delta{E_{полн}}=2\mu_БB=2\cdot5,762\cdot10^{-5}\frac{эВ}{Тл}\cdot1Тл=115,9\cdot10^{-6}эВ\approx116 \)мкэВ. |
|
\( \delta{E_{полн}}=4\mu_БB=4\cdot5,762\cdot10^{-5}\frac{эВ}{Тл}\cdot1Тл=231,7\cdot10^{-6}эВ\approx232 \)мкэВ. |
г) Для дублетного 2D5/2 - терма L=2, S=1/2, J=5/2.
Вычислим множитель g Ланде
\( \mathrm{g}=\frac{3}{2}+\frac{S(S+1)-L(L+1)}{2J(J+1)}=\frac{3}{2}+\frac{3-2\cdot3\cdot4}{2\cdot5\cdot7}=\frac{84}{70}=\frac{6}{5} \). |
Полное расщепление δEполн терма вычисляется формулой (2). Оно равно
\( \delta{E_{полн}}=2\cdot5,796\cdot10^{-5}\cdot\frac{6}{5}\cdot1\cdot\frac{5}{2}=3,4777\cdot10^{-4}=347\cdot10^{-6}=348 \)мкэВ. |

