2. Волновые свойства вещества
Задача №4.
Частица массы m находится в одномерной прямоугольной яме потенциальной яме с бесконечно высокими стенками. Ширина ямы l. Найти возможные значения энергии частицы, имея в виду, что реализуется лишь такие состояния ее движения, для которых в пределах данной ямы укладывается целое число дебройлевских полуволн.
|
Дано: l, m |
Решение: 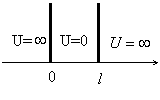 |
|---|---|
|
Найти: En=? |
По условию задачи имеем
\( l=n\frac{{\lambda}_n}{2} \), n=1,2,... |
(1) |
Полная энергия частицы равна
E=T+U, |
(2) |
Внутри ямы частица движется свободно, то есть ее потенциальная энергия U=0. Следовательно, полную энергию частицы составляет ее кинетическая энергия
\( E=\frac{p^2}{2m} \). |
(3) |
Используя соотношением де Бройля для длины волны и импульса частицы с учетом условия (1) найдем энергетические уровни частицы в яме
\( E_n=\frac{h^2}{8ml^2}n^2 \). |
(4) |
Учитывая соотношение между константой h Планка и константой ћ Планка - Дирака, запишем (4) в следующем виде:
\( E_n=\frac{{\pi}^2{\hbar}^2}{2ml^2}n^2 \). |
(5) |

