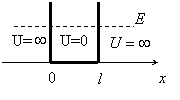3. Уравнение Шредингера. Волновая функция
Задача №2.
Найти пси - функции и значения энергии частицы массы m, находящейся в одномерной бесконечно глубокой потенциальной яме ширины l.
|
Дано: m, l |
Решение: |
|---|---|
|
Найти: ψn=? En=? |
Потенциальная яма есть график одномерной ступенчатой функции потенциальной энергии частицы
|
(1) |
График функции (1) имеет вид
|
Вне ямы (x≤0, x≥l) функция ψ(x) равна нулю. Движение частицы в яме описывается одномерным уравнением Шрёдингера
\( \frac{d\psi(x)}{dx^2}+\frac{2m}{{\hbar}^2}E\psi(x)=0 \). |
(2) |
Дополнительными условиями в задаче будут следующие граничные условия:
ψ(0)=ψ(l)=0. |
(3) |
Вводим новый параметр уравнения
\( {\omega}^2=\frac{2mE}{{\hbar}^2} \). |
(4) |
Тогда уравнение примет вид
\( \frac{d \psi(x)}{dx^2}+{\omega}^2\psi{x}=0 \). |
(5) |
Известно, что такое уравнение имеет действительные решения
ψ(x)=Asinωx+Bcosωx. |
(6) |
Необходимо определить коэффициенты A,B и параметр ω. Чтобы соблюсти условие ψ(0)=0, полагаем что, B=0. Из второго граничного условие следует, что
\( \omega= \pm\frac{n\pi}{l}, n=0,1,... \) |
(7) |
Используя полученное выражение (7), из определения (4) параметра ω находим выражение для возможных энергетических уровней частицы, движущейся в бесконечно глубокой потенциальной яме
\( E_n=\frac{{\pi}^2{\hbar}^2}{2ml^2}n^2 \), n=1,2,... |
(8) |
Найденным собственным значениям энергии En соответствуют собственные волновые функции ψn(x) вида
\( { \psi }_n(x)=Asin\frac{n\pi}{l}x \). |
(9) |
Из условия нормировки волновой функции к единице
\( A^2{\int}_{0}^{l}{sin}^2\frac{n\pi}{l}xdx=1 \) |
(10) |
находим коэффициент A. Вычислив интеграл (10), получим
\( A=\sqrt{\frac{2}{l}} \). |
(11) |
Итак, выражение для собственных функций ψn(x) энергии частицы в бесконечно глубокой потенциальной яме имеет вид
\( {\psi}_n(x)=\sqrt{\frac{2}{l}}sin\frac{n\pi}{l}x \), n=1,2,... |
(12) |