3. Уравнение Шредингера. Волновая функция
Задача №5.
Найти вероятность просачивания электрона через потенциальный барьер шириной 5 Å и высотой 0,4 эВ, если он разгоняется электрическим полем 0,3В.
|
Дано: U0=0,4 эВ, φ=0,3 эВ, l=5 Å |
Решение: 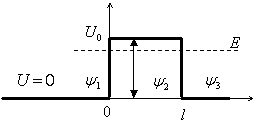 |
|---|---|
|
Найти: P=? |
Потенциальный барьер конечной ширины разделяет пространство на три смежные области, в которых состояние частицы описывается тремя различными функциями. В соответствии с этим имеем три уравнения Шрёдингера:
\( \frac{d^2{\psi}_1}{dx^2}+k_1{\psi}_1=0 \) для первой области, |
(1) |
\( \frac{d^2{\psi}_2}{dx^2}-k_2{\psi}_2=0 \) для второй области, |
(2) |
\( \frac{d^2{\psi}_3}{dx^2}+k_3{\psi}_3=0 \) для третьей области. |
(3) |
Для первой и третьей областей ввели обозначения коэффициентов
\( k_1^2=k_3^2=\frac{2mE}{{\hbar}^2} \). |
(4) |
При учете условия E<U0 аналогичный коэффициент для второй области имеет вид
\( k_3^2=\frac{2m(U_0-E)}{{\hbar}^2} \). |
(5) |
Общие решения уравнения в трех смежных областях:
ψ1=A1eik1x+B1e-ik1x для первой области, |
(6) |
ψ2=A2ek2x+B2e-k2x для второй области, |
(7) |
ψ3=A3eik3x+B3e-ik3x для третьей области. |
(8) |
В двух первых областях часть падающих частиц отражаются обратно, а в третьей такого отражения нет. Следовательно, коэффициент B3 нужно приравнять нулю. Чтобы найти соотношения, связывающие амплитудные коэффициенты A1,B1,A2,B2,A3, необходимо использовать условия «сшивания» функций на границах областей:
ψ1(0)=ψ2(0), ψ2(l)=ψ3(l) |
(9) |
\( \frac{d\psi_1}{dx}|_{x=0}=\frac{d\psi_2}{dx}|_{x=0} \), \( \frac{d\psi_2}{dx}|_{x=l}=\frac{d\psi_3}{dx}|_{x=l} \). |
(10) |
Тогда получим систему алгебраических уравнений
A1+B1=A2+B2, |
(11) |
A2ek2l+B2e-k2l=A3eik3l, |
(12) |
ik1A1-ik1B1=k2A2-k2B2, |
(13) |
k2A2ek2l-k2B2e-k2l=ik3A3ek3l. |
(14) |
Вероятность просачивания частицы через потенциальный барьер определяется коэффициентом D прозрачности барьера
\( D=\frac{{|A_3|}^2}{|A_1|}=\frac{A_3^*A_3}{|A_1|} \). |
(15) |
Следовательно, нас интересуют коэффициенты A3 и A1. Поскольку падение частицы на барьер является достоверным событием, можно полагать амплитуду A1 волны, падающей на барьер, равным единице. А коэффициент A3 можно найти, решая систему уравнений (11) - (14). Для этого необходимо из системы (11) - (14) составить систему из трех уравнений, первое из которых имеет вид
1+B1=A2+B2. |
(11a) |
Умножим уравнение (11а) на мнимую единицу i и сложим с уравнением (13). Это дает второе искомое уравнение
(n+i)A2-(n-i)B2=2i, |
(16) |
где n=k2/k1. Теперь умножим уравнение (12) на число i и вычтем его из уравнения (14). В результате получим
(n-i)ek2lA2-(n+i)e-k2lB2. |
(17) |
Корни системы (11а -17) имеют вид
\( A_2=\frac{2i(n+i)e^{-k_2l}}{{(n+i)}^2e^{-k_2l}-{(n-i)}^2e^{k_2l}} \), |
(18) |
\( B_2=\frac{2i(n-i)e^{k_2l}}{{(n+i)}^2e^{-k_2l}-{(n-i)}^2e^{k_2l}} \), |
(19) |
\( A_3=\frac{4ine^{-ik_1l}}{{(n+i)}^2e^{-k_2l}-{(n-i)}^2e^{k_2l}} \). |
(20) |
Обычно условие k2l>>1 выполняется, поэтому первым слагаемым в знаменателе дроби (20) можно пренебречь. Тогда имеем
\( A_3\approx-\frac{4ine^{-ik_1l}}{{(n-i)}^2}e^{-k_2l} \). |
(21) |
Поставляя (21) в (15), находим
\( D\approx-\frac{4ine^{-ik_1l}}{{(n-i)}^2}e^{-k_2l}{\cdot}\frac{4ine^{ik_1l}}{{(n+i)}^2}e^{-k_2l}=\frac{16n^{2}}{{(n^2+1)}^2}e^{-2k_2l} \). |
(22) |
Здесь учтено, что \( {|n-i|}^2=(n-i)(n+i)=\sqrt{n^2+1} \).
Следовательно, имеем
\( D\approx\frac{16n^{2}}{{(n^2+1)}^2}e^{-\frac{2}{\hbar}\sqrt{2m(U_0-E)}l} \). |
(23) |
Вычислим величину n2, выразив ее через величины U0 и E:
\( n^2=\frac{k_2^2}{k_1^2}=\frac{U_0-E}{E}=\frac{U_0}{E}-1=\frac{0,4}{0,3}-1=0,333 \). |
Расчет:
\( D=\frac{16\cdot{0,333}^2}{{(0,333+1)}^2}\cdot{exp}\left(\frac{2\cdot5\cdot10^{-10}}{1,0546\cdot10^{-34}}\cdot\sqrt{2\cdot0,911\cdot10^{-30}\cdot(0,4-0,3)\cdot1,6\cdot10^{-19}}\right)=0,9985\cdot{exp}(-1,618999)=0,9985\cdot0,198097=0,19779\approx0,2=20 \)% |
По поводу полученного результата сделаем следующее замечание. Расчет показал, что коэффициент перед экспонентой имеет величину порядка единицы. В данном случае это не является исключением. Поэтому в формуле (23) не пишут его как несущественный множитель, и коэффициент просачивания частицы через прямоугольный барьер конечной ширины представляют в виде
\( D\approx{e}^{\frac{2}{\hbar}\sqrt{2m(U_o-E)}l} \). |
(24) |

