5. Молекулы и кристаллы

ПредыдущаяСледующая

Задача №3.

Найти отношение энергий, которые необходимо затратить для возбуждения двухатомной молекулы HI на первый колебательный и первый вращательный уровни.

 

Дано:

HI

Решение: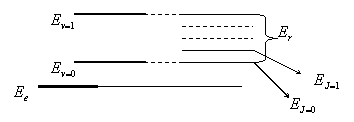

Найти:

\( \eta =\frac{\Delta{E}_1^{кол}}{\Delta{E}_1^{вр}} \)=?
 

В первом приближении молекулы могут колебаться и вращаться относительно общего центра инерции независимо друг от друга. Так колебательная энергия Ev, соответствующая колебаниям молекулы, определяется выражением

 

\( E_{\nu}=\left(\nu+\frac{1}{2}\right)\hbar\omega \) (v=0,1,...),

(1)

где v - колебательное квантовое число, ω - собственная частота колебаний молекулы, определяемая как частота осциллятора \( \omega=\sqrt{k/m} \). А вращательная энергия Er, связанная вращением молекулы в целом, квантуется по формуле (1) задачи 2.

Определим энергию перехода на первый колебательный уровень:

 

\( \Delta{E}_1^{кол}={E}_1^{кол}-{E}_0^{кол}=\frac{3}{2}\hbar\omega-\frac{1}{2}\hbar\omega=\hbar\omega \).

(2)

Энергия перехода на первый вращательный уровень равна

 

\( {E}_1^{вр}=\frac{\hbar^2}{I} \).

(3)

Выражение для искомой величины η имеет вид

 

\( \eta=\frac{\omega{I}}{\hbar}=\frac{\omega\mu{d}^2}{\hbar} \).

(4)

Приведем табличные данные: ω=4,350·1014c-1, d=1,604·10-10 м, mH=1,007825 а.е.м., м, mI=126,9045 а.е.м.

Расчет:

 

   \( \mu=\frac{1,007825\cdot126,9045\cdot{(1,660\cdot10^{-27})}^2}{1,007825+126,9045)\cdot1,660\cdot10^{-27}}=1,66\cdot10^{-27} \)кг,

            I=1,66·10-27·(1,604·10-10)2=4,2678·10-47кг·м2,

\( \eta=\frac{4,26783\cdot10^{-47}\cdot4,350\cdot10^{14}}{1,0546\cdot10^{-34}}=17,609\approx1,76\cdot10^2 \).

ПредыдущаяСледующая